FIR 是数字信号处理中一种非常的常见运算。我在学校还在上 VHDL 课时,就被要求写这玩意儿。当然当时我 messed up everything, and no one loves me 就是另外一回事儿了。
一个
$$N$$阶的 FIR 滤波器的时域表达式为:
$$y[n] = \sum_{i = 0}^{N}{h_i \cdot x[n-D-i]}$$其中
$$x[n]$$是输入信号,
$$y[n]$$是输出信号,
$$h_i$$是 FIR 滤波器的系数。
$$D$$是一个常数,代表处理的延迟。从公式上来看,FIR 本质上就是一维卷积运算,暴力相乘然后相加。每计算一个
$$y[n]$$需要
$$N$$次乘法和
$$N-1$$次加法。
FIR 的结构取决于很多因素,包括滤波器阶数,时钟速率,吞吐率等等。比较典型的例子是在吞吐率要求非常低时,可以采用 MACC(乘累加)结构;而吞吐率较高时采用多相结构。一般来说 FPGA 中的 FIR 是一个面积敏感的结构,它会消耗比较多 MAC(硬核乘法器)的数量。一个简单的乘法器数量
$$k_{MAC}$$的估算公式是:
$$k_{dsp} = ceil(\frac{(N+1)f_t}{f_{clk}})$$其中
$$f_t$$是 FIR 模块的吞吐率,
$$f_{clk}$$是时钟频率,其比值代表了硬件的过采样倍数。例如一个采样率为
$$100 MHz$$的数据采集系统,需要对采集到的信号进行滤波,FIR 的阶数是 7。为了保证能够连续不断的处理,模块的吞吐率至少和采样率相等。如果 FPGA 比较低端,那么时钟可能也会选择
$$100 MHz$$。最终可以得出
$$k_{dsp}=8$$。在不知道滤波器系数特性时,在资源就已经无法优化了。在结构上,FIR 有很多合适的结构,其中一种如下图所示:
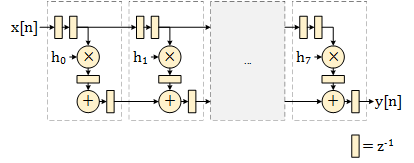
这种结构被称为脉动式(Systolic)结构,它在每个乘或加操作之后都有寄存用于改善时序。在 FIR 的设计中有一个计算的方法:每个寄存器都是
$$z^-1$$;当
$$x[n]$$经过
$$z^-1$$之后就会变成
$$x[n-1]$$。因此可以轻松写出输出:
$$y[n] = h_0 \cdot x[n-11] + h_1 \cdot x[n-12] + \cdots + h_7 \cdot x[n-18]$$并且
$$D = 11$$。至此我们完成了一个通用 FIR 滤波器。接下来我们可以讨论下一些特殊结构的 FIR(TBD):
- 线性相位(Linear phase)
- 半带(Half-band)与 2 倍插值/抽取
- 分数倍插值/抽取